Bohyun Yoo (MBA AI/BigData, 2023)
The real estate market is showing unusual signs. As global tightening begins, experts worry that the bubble in the domestic real estate market, which benefited from the post-COVID-19 liquidity, may burst. They warn we should prepare for a potential impact on the real economy.
Since late last year, major central banks, including the U.S. Federal Reserve, have been raising interest rates to combat inflation. This has caused housing prices to decline, reducing household net worth and increasing losses for real estate developers, which could potentially trigger a recession.
Global Liquidity and the Surge in Housing Prices
Meanwhile, some investors are attempting to exploit the 'bubble' in the real estate market for profit. They expect prices to fall soon and aim for capital gains by buying low. Others seek arbitrage opportunities, assuming prices haven’t yet aligned with fair value. For these investors, it is crucial to assess whether current property prices are discounted or overpriced compared to intrinsic value.
Similarly, for financial institutions heavily involved in mortgage lending, analyzing the real estate market is key to the success of their loan business. This study examines why identifying the 'bubble' in the real estate, especially in auctions, is important and how it can be explored mathematically and statistically.
Importance of Real Estate Auction Market
Various stakeholders participate in Korea's real estate auction market, each with distinct objectives. Homebuyers, investors seeking profit opportunities, and financial institutions managing mortgages are all active players. The apartment auction market, in particular, is highly competitive, with prices often closely aligned with those in the regular sales market.
Financial institutions are closely connected to the auction market. In Korea, when a borrower defaults on a property loan, the property is handled through court auctions or public sales overseen by the state. Financial institutions recover the loan amount by selling the collateral through these auctions in the event of a default.
Therefore, one of the key factors for financial institutions in determining their lending limits is how much principal they can recover in the auction market in the event of a default, especially for fintechs (P2P lending) and secondary lenders such as savings banks and capital, which are not subject to loan-to-value (LTV) restrictions.
Since most financial institutions hold a significant portion of their assets in mortgage loans, lending the maximum amount within a safe limit is ideal for maximizing revenue. Thus, when financial institutions review mortgage loan limits, trends in the auction market serve as a critical decision-making indicator.
To See Beyond Prices in the Market
It's easy to assume that the winning bid for an apartment auction in a certain area of Seoul, at a particular time, would either come at a discount or a premium compared to the general market price. And, with a bit of rights analysis, setting a cautious upper limit wouldn't be all that hard. But, in reality, it's a bit more complex than just making those assumptions.
Furthermore, if we want to examine the market movement from a broader perspective rather than focusing on individual auction cases, we need to change our approach. For example, it's easy to track Samsung’s stock price trends in the stock market, even down to minute-by-minute data over the past year. However, in real estate, auctions for a specific apartment, like Unit 301 of Building 103 in a particular complex, don’t happen every month. Even expanding the scope to the whole complex yields similar results. Therefore, it's no longer feasible to analyze the market purely based on prices. Real estate analysis must shift from a [time-price] perspective, as in stocks, to a [time-location] perspective.
Errors in the Auction Winning Bid Rate Indicator
Just as the general sales market has a time-series index like the apartment sales index, the auction market has the winning bid rate indicator. This is a monthly indicator published by local courts, showing the ratio of auction-winning bids to court-appraised values in a given area. For example, if the court appraises a property at 1 billion won and the winning bid is 900 million won, the winning bid rate would be 90%.
Since court appraisals are generally considered market prices, the winning bid rate represents the ratio of the auction price to the market price. When calculated for all auctions in an area, it gives the average auction price compared to the market value for that month.
However, this indicator has significant flaws. The court appraisal is set when the auction begins, but the winning bid reflects the price at the time of the auction. Given that auctions typically take 7 to 11 months, this time gap can lead to errors if market prices drop or rise sharply. For instance, news reports during recent price surges claimed that the winning bid rate in Seoul exceeded 120%, which seems hard to believe—how could auction prices be 1.2 times higher than market prices? This is actually incorrect information.
If market prices rise sharply during the 7 to 11 months it takes to complete an auction, bidders place their bids based on current market prices, while the court appraisal remains fixed at the start. As a result, the appraised value becomes relatively lower compared to the current market price, creating the illusion of a 120% winning bid rate. Interpreting this rate at face value can lead to poor real estate decisions or significant errors.
Limitations of Previous Studies
This has prompted previous auction market studies to try addressing the shortcomings of the winning bid rate indicator. For instance, some researchers adjusted the court-appraised value—the denominator—by factoring in the sales index at the time of the auction, aiming to estimate a more accurate "true winning bid rate."
However, experts agree this is not a perfect solution. To estimate the true winning bid rate for Seoul, all auctions during that period would need to have their court appraised values corrected. Each auction has different appraised values and closing dates, and researchers would have to manually correct hundreds or thousands of auctions. Expanding the region would make this task even more challenging, and even if corrected, the values would only be approximations, not guarantees of accuracy.
If researchers selectively sample auctions for convenience, it could introduce sampling bias. This is similar to trying to find the average height of Korean men by only sampling from a tall group.
It highlights the need for time-series indicators from a market perspective when making business decisions, rather than focusing solely on price data. The winning bid rate, commonly used in auctions, is prone to errors. Although methods like adjusting the court-appraised value have been suggested, they are difficult to apply in real-world scenarios.
These are the same problems I encountered as a practitioner. When time-series analysis was needed for decision-making, the persistent issues with the winning bid rate made it hard to use effectively.
Winning Price vs. Winning Bid Rate
There is an important distinction to make here. Analyzing the auction "winning price" and analyzing the "winning bid rate" have different meanings and purposes. As mentioned earlier, analyzing the winning price of a single auction case poses no issue.
For example, focusing on apartments, bidders base their bids on the market price at the time of bidding. If the gap between the bidding and final winning is about 1 to 2 months, considering that real estate prices don’t fluctuate dramatically like stocks within a month, the winning price should not significantly deviate from the market price a couple of months earlier. Factors like distance to schools, floor level, and brand, which are known to affect market prices, are likely already reflected in the market price, meaning they won't heavily impact the auction winning price.
Most prior studies on real estate auctions, particularly for apartments, have concentrated on how accurately they can predict the "winning price" and identifying the key factors that influence it. However, in practice, as previously discussed, price prediction is not the primary concern.
Even a simple linear regression analysis reveals that the R-squared between winning prices and KB market prices from 1-2 months earlier exceeds 95%, indicating a strong linear relationship. There is no evidence of a non-linear connection. If future trend forecasting is needed, the focus should shift toward a time-series analysis.
Discounts/Premiums Changing Over Time
After a lengthy introduction, let's get to the main point—I want to analyze the auction market. The problem is, the data contains significant errors, and trying to correct them individually has its limitations, especially within the industry. We need a different approach. So, what alternative methods can we use? And what insights can this new analysis reveal?
This is the core topic and background of the study. I used statistics as a tool to solve a seemingly insurmountable business problem encountered in practice.
What I aimed to find in the market was the difference between the sales market and the auction market. This 'difference' can be expressed as the discount or premium of the auction market compared to the sales market. Additionally, a time-series analysis is essential because the discount/premium factors will change over time depending on the economic or market conditions.
Factors of Discount/Premium in the Auction Market
Existing studies on the factors of discount/premium in housing auctions are quite varied. Nonetheless, as mentioned earlier, both international and domestic research mainly focus on price analysis rather than market analysis, making it difficult to grasp the broader trends of real estate. Typically, they gather auction cases over several years, remove legal issues, compare with market prices, and conclude there was a discount/premium, attributing it to specific factors.
Moreover, overseas studies often allow private auctions and use bidding systems, making direct application to Korea difficult. In domestic studies, the few that exist lack market-based analysis.
The Challenge: 'Data Availability'
If we assume that there is a discount/premium factor in the auction market compared to the sales market, the auction sale rate can be restructured as follows:
[ Auction Sale Rate{t} = \frac{\sum Market Price{t} \pm Premium{t}}{\sum Appraisal Price{t-n}} ]
Now, interpreting the three elements of the auction sale rate as influential factors and transforming it into a linear regression model, it would look like this:
[ Auction Sale Rate{t} = \beta{0} + \beta{1} EoM{t} + \beta{2} EoA{t} + \beta{3} EoP{t} ]
- EoM: Effect of Market Price (influence of the general sales market)
- EoA: Effect of Appraisal Price (influence of court appraised values)
- EoP: Effect of Price Premium (influence of discount/premium)
To complete this regression model, data for all three variables is needed. The effect of market prices can be substituted with the sales index provided by the Korea Real Estate Board. The sales index should be transformed using a log difference to match the format of the auction sale rate.
A major challenge lies in obtaining data for the other two variables. First, acquiring court-appraised price data for research purposes is nearly impossible. The focus here isn't on the historical 'appraised price' itself, but rather on how much it influenced each analysis period (typically monthly). This means we need data adjusted to the auction's closing time. However, without digitizing all auction cases nationwide over the past 10 years, this task is virtually unachievable. The unobservable variables are intertwined, resembling a noisy background.
Factor Separation and Extraction
How can we isolate a specific male voice from a noisy mix of sounds? This is where the Fourier Transform comes in. It converts an input signal from the time domain to the frequency domain, separating each individual frequency. By applying an inverse Fourier Transform, we can find the unique voice, leaving it intact while setting other elements to zero, effectively filtering out noise.
In the same way, if we view the auction sale rate as a noisy input signal, we can separate its contributing factors independently. First, by removing the effect of market prices from the auction sale rate using a regression model, we can assume that the residual term contains hidden influences from court appraisals and discount/premium factors. Among the remaining elements in the residuals, we can assume the two strongest factors are the court appraised price and discount/premium. Fourier Transform can then be used to extract these two independent signals.

This assumption can be statistically verified. As shown in the table, when regressing the auction sale rate using the three initially assumed variables—two components extracted by Fourier Transform and the market price data—the adjusted R-squared is about 94%. In other words, the auction market can be explained by these three factors (market price, court appraisal, and discount/premium). Additionally, the ACF/PACF plot of the residuals after Fourier extraction (see figure below) shows no significant remaining patterns.
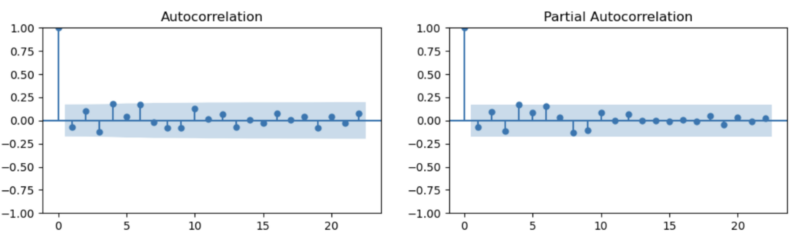
Through the Fourier Transform, I was able to resolve both the limitations of the auction sale rate as a time-series data and the issue of relying on external data. I successfully extracted the two remaining factors (court appraisal and discount/premium) from the residuals after removing the effect of market prices.
However, I must caution that using Fourier Transform on general asset market data, like stocks or bonds, is risky. This method is only applicable to data with consistent cycles. Unlike price or sales indices, auction sale rate data exhibits cyclic movements between 80-120%, driven by economic and market conditions, allowing the process to be performed without errors.
Court Appraisal Extraction
The two factors extracted through the Fourier Transform are currently only assumptions, believed to represent court appraised value and the discount/premium factor. Therefore, it is necessary to accurately verify if these factors are indeed related to court appraised values and discount/premium factors. First, I analyzed two aspects using around 2,600 auction cases:
- The average time gap between the court appraisal date and the auction closing date.
- The relationship between court appraisal prices and KB market prices at the appraisal date.
The time gap between appraisal and auction ranged from 7 to 11 months (within the 25% to 75% range), and the relationship between the court appraisal price and KB market price showed a Beta coefficient of 1.03, indicating almost no difference. Based on these two results, I reached the following conclusions:
- There is a lag relationship between court appraisal prices and market prices (lag = time gap).
- The lag variable of market prices can substitute for court appraisal prices.
Regression analysis showed that the lag variable of the sales index and court appraisal had about 54% explanatory power. This confirmed that the court appraisal component extracted via Fourier Transform could function as an actual court appraisal. Additionally, when comparing how well the lag variable and court appraisal component explained the auction sale rate, the appraisal component (50%) outperformed the lag variable (20%).
Discount/Premium Extraction
Next, I tested the discount/premium component, the core of this study, from two angles. First, whether the component extracted by the Fourier Transform can function as a discount/premium factor, and second, what the true identity of this component is.
For verification, I applied a sigmoid function to the discount/premium component to produce an on/off effect (0/1).
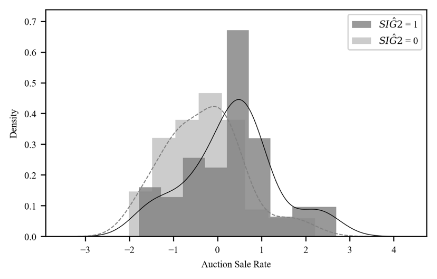
I attempted to compare this component with various data available from sources like the National Statistical Office, but I couldn't find any data showing similar patterns. The reason for this was simpler than expected.
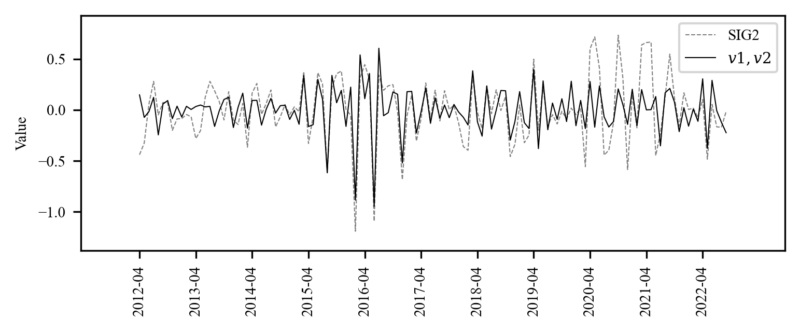
The auction market is dependent on the sales market. Most macroeconomic variables we know likely influence housing prices, which have already been removed from the regression model. Therefore, the remaining factors are likely unique to the auction market, independent of sales prices. The variable that shows a similar pattern to the discount/premium component is the month-over-month and two-month differences in the winning bid rate, as shown in the figure.
The Nature of the Discount/Premium
To summarize the analysis so far: after excluding the effects of market prices and court appraisals, the remaining factor in the auction sale rate is the discount/premium factor. This factor exhibits a similar pattern to the month-over-month fluctuations (volatility).
In other words, if past volatility explains what the 'sales price' and 'court appraisal' couldn't, it suggests that the auction market has a discount/premium factor driven by volatility (the difference in past winning bid rates). As I will explain later, I have named this component the 'momentum factor,' believing it to explain trends.
Cluster Characteristics of the Momentum Factor
As we delve deeper into this analysis, it's essential to recognize that auction market dynamics are not static but evolve over time, necessitating a more adaptive model to track these changes effectively.
Unlike Ordinary Least Squares (OLS) regression, which assumes a fixed beta coefficient, the Kalman Filter's state-space model allows the beta coefficient to change over time. By tracking this time-varying coefficient, we can observe how the influence of different variables fluctuates over various periods. To analyze the 'momentum factor' in greater detail, I applied the Kalman Filter to assess whether the beta coefficient indeed varies over time.
Consequently, as shown in the figure below, we can observe that the regression coefficient of the momentum factor exceeds that of the sales price regression coefficient in certain intervals. Upon examining these intervals, it becomes clear that the momentum factor exhibits a type of clustering effect.
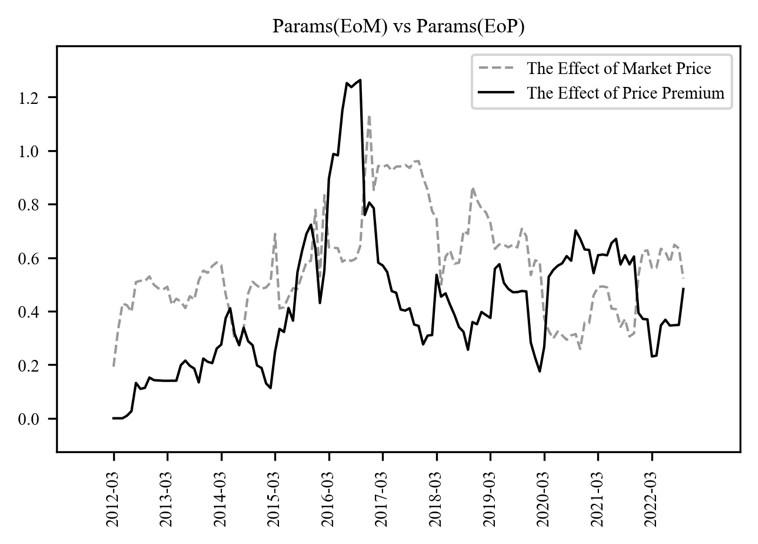
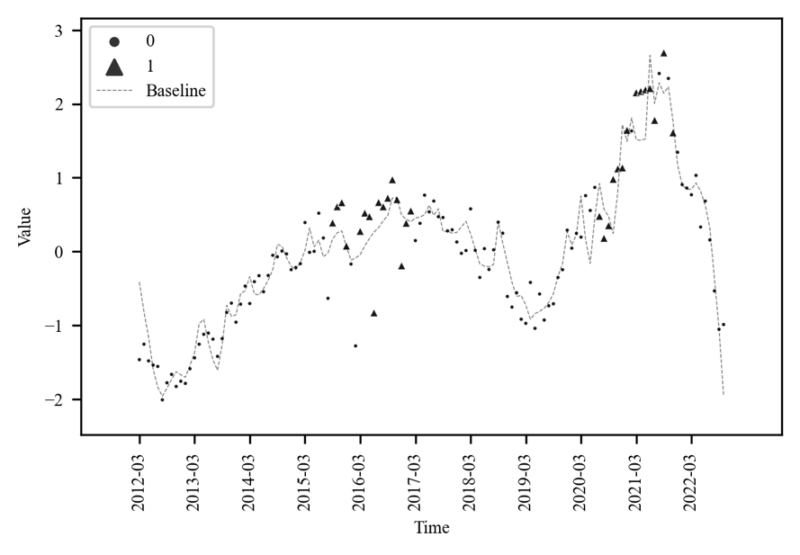
The True Meaning of the Momentum Factor
We need to think more deeply about the "intervals where the momentum factor's sensitivity exceeds market prices." The momentum factor explains the discount/premium. Therefore, when the discount/premium factor significantly impacts the auction sale rate, it suggests that the usual "average relationship" between the sales market and the auction market has been disrupted.
What does it mean when the "average relationship is disrupted"? For example, if the sales and auction markets typically maintain a gap of 10, this disrupted relationship means the gap has shrunk to 5 or expanded to 15. Such situations typically occur during overheated or excessively cooled markets, or just before such conditions arise. When everyone is rushing to buy homes, this can naturally lead to an "overheating" that breaks the usual relationship, which can be interpreted as increased "popularity" in the auction market.
However, one important thing to note is that when the sales market falls, the auction market typically falls too. This is because the market price has the largest influence on changes in the auction sale rate. In other words, even if the momentum factor is inactive, the auction market can rise or fall in response to the sales market. Therefore, the "activation of the momentum factor" doesn't necessarily indicate price increases or decreases.
The discount/premium factor is ultimately defined as the effect of market prices + '@'. The sensitivity analysis of the discount/premium factor indicates that '@' represents "excessive movement beyond the average." I named this the "momentum factor" because I believe it can detect changes in market sentiment or trends. As seen in the Figure 5, the momentum factor tends to signal market trend changes before and after its cluster periods.
I cautiously suggest that when the momentum factor shows excessive movement, it could signal a "bubble" or "cooling" sign. Further exploration of this idea is beyond the scope of this [paper discussion], but it certainly warrants future research.
Focus on Logic Over Technique
The reason I wrote this paper wasn't because I majored in real estate or specialized in the field. Most of my work in recent years involved changing systems to enable data-driven decision-making, one of which was loan screening, and another was related to real estate.
I understand that definitions of data science vary from person to person. However, for me, data science was the perfect tool for solving business problems. That’s why I chose a topic that was considered insurmountable in practice and applied the knowledge I learned in school.
The aspect I want to highlight in this paper is not the technical side but the logical one. The techniques used—regression analysis, Fourier transformation, and the Kalman filter—are not particularly advanced for graduate-level science and engineering. There was also an incentive to avoid using non-linear pattern matching techniques like ML/DL, which are unsuitable for financial data requiring clear interpretations. For me, it was more important to choose the method suited to the problem, and nothing more. The key was how to logically solve and approach this issue.
I believe that in solving business problems, logic should come first, and technology is just a tool. This is my ideal approach, and I wanted to keep the paper's concept simple, yet logically solid.
The Gap Between Business and Research
When I started researching for this paper, I remember thinking, "What problem should I try to solve?" My obsession with problem-solving came from the belief that there is a gap between the worlds of business and research, a bias I developed through experience.
As a practitioner, I think that in most fields, decisions are still largely based on subjective judgment rather than data. Furthermore, I know that many industries face challenges in successfully adopting data analysis systems, and I personally experienced this. While each field has its own circumstances, I believe one key reason for this gap is the disconnect between research and business.
From the industry perspective, I often felt that many research results focused on the study itself, neglecting "real-world applicability." On the other hand, from an academic perspective, I found that business often relied too heavily on subjective decisions, ignoring the complexities of the real world.
Bridging the Gap
Thus, the real intent of this paper was to bridge the gap between business and research, however small that contribution may be. I wanted to be a "conceptualizer" who actively uses data analysis to solve business problems. In this sense, I believe this paper sits somewhere between research and business. Throughout the writing process, I fought hard against the temptation to get lost in academic curiosity, focusing instead on practical applicability.
The quality and results of the paper will be judged by reviewers or proven in real-world industries, not by me. However, I anticipate that my future work will also be positioned between these two worlds. Connecting these two domains is an incredibly fascinating challenge. To view the article in Korean, please clickhere.